Researchers from the Beijing Computational Science Research Center, including Guolin Nan, Zhijian Li, Feng Mei, and Zhihao Xu, have recently published a study on anomalous localization in non-Hermitian quasicrystals with disordered imaginary gauge fields. Their work was published in the journal Physical Review Letters.
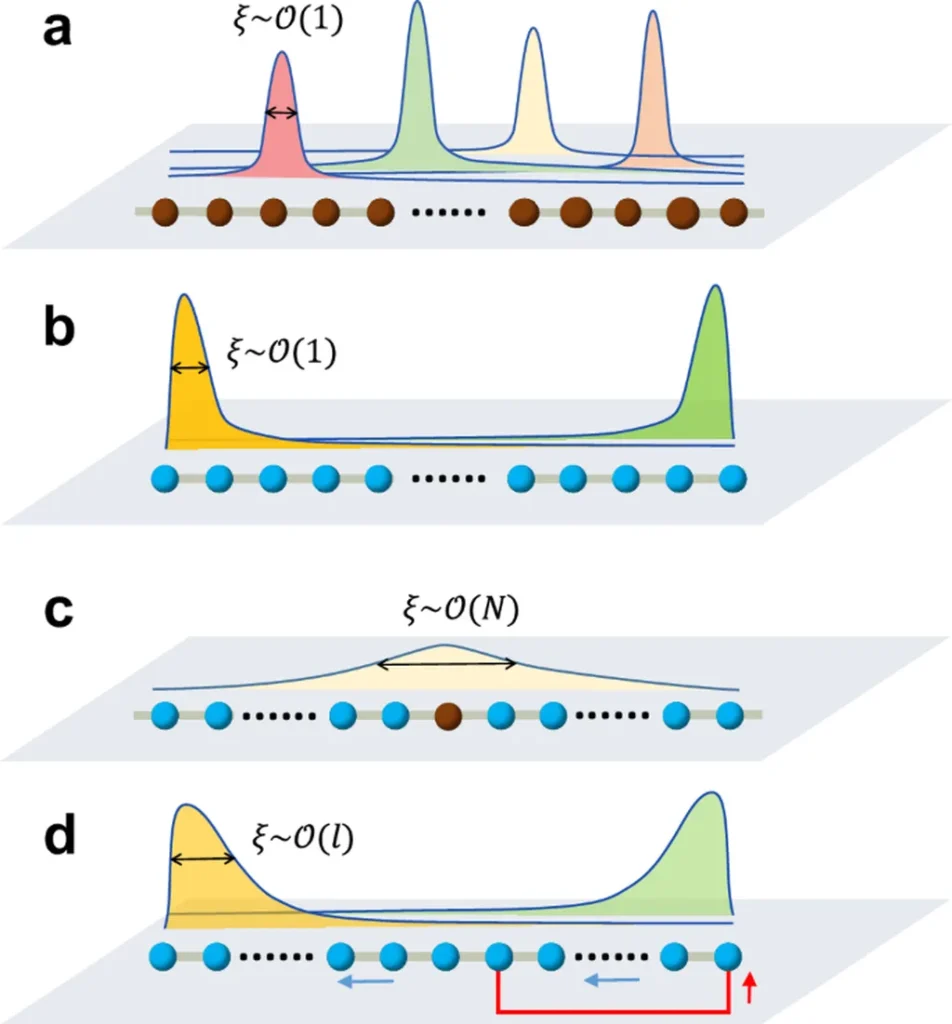
The team investigated a one-dimensional non-Hermitian quasicrystal system, specifically a generalized Aubry-André-Harper (AAH) chain. This system features asymmetric nearest- and next-nearest-neighbor hoppings, generated by a Bernoulli imaginary gauge field and a quasiperiodic onsite potential. In simpler terms, they studied how particles move and localize in a complex, disordered, and non-Hermitian (a mathematical term indicating that the system does not conserve energy) environment.
The researchers found that the system undergoes a transition from a phase with a non-Hermitian skin effect (ENHSE), where particles tend to accumulate at the boundaries, to a fully localized phase, where particles are trapped in specific regions. Interestingly, they discovered that the fractal dimension, a common measure used to distinguish phases, is not effective in this case. Instead, they proposed using the Lyapunov exponent and center-of-mass fluctuations as better diagnostic tools.
Moreover, the transition is accompanied by a change in the spectrum of the system from complex to real values under periodic boundary conditions and a topological change of the spectral winding number. When they introduced next-nearest-neighbor hopping, they found an anomalous mobility edge. This edge separates Anderson-localized states, where particles are trapped, from ENHSE states, rather than the typically expected extended states, where particles can move freely.
The researchers also proposed a practical dynamical probe based on wave-packet expansion. This probe can help identify the different phases and transitions by observing the behavior of a wave packet over time. For typical disorder realizations, the dynamics show winding-controlled drift and disorder-selected pinning or boundary-wrapping recurrence. However, when averaged over many disorder realizations, the transport behavior resembles that of a Hermitian system.
The findings of this study offer practical spectral, topological, and dynamical diagnostics for understanding anomalous localization and mobility edges in non-Hermitian quasicrystals. While the direct application to the energy sector may not be immediately apparent, the insights gained from this research could potentially contribute to the development of advanced materials and technologies for energy storage and transfer, where understanding and controlling particle behavior is crucial.
This article is based on research available at arXiv.